Triquetras, Trefoils, and Topological Awesomeness

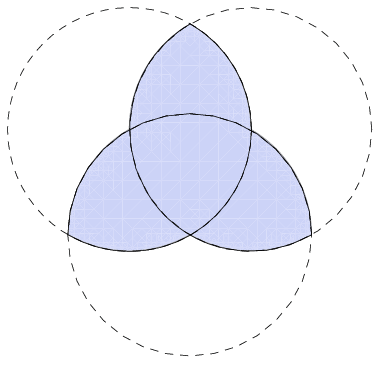
Here is a pretty awesome piece of mathematically interesting art I saw the other day. 

This shape is called a triquetra. The name comes from the Latin tri- meaning "three" and quetrus meaning "cornered." 

It is analogous to the trefoil knot - what you get when you tie a simple overhand knot and join the two ends. 

Another way to find a triquetra is to look at the intersection of three circles, like a Venn diagram. (Note that the shape formed at the very center is a Reuleaux triangle, a shape of constant width, deserving of a blog post all of its own...another day)

The triquetra is often shown interlaced with a circle and is common to Celtic art. It has many meanings throughout various religions and symbolizes things that are threefold - mind, body, soul; past, present, future; Father, Son, Holy Spirit; to name a few. 

And if that wasn't cool enough, here's another cool thing you can do - take a strip of paper, give it three half-twists, and join the two ends into a three twist Möbius strip. 

Then, cut the strip in half along the middle of the strip. After some rearranging and playing with the twists, BAM! Trefoil! How awesome is that? 

For further exploration: 

• Draw a triquetra - link 
• Animation of Möbius strip to trefoil knot - link
• George Hart shows how to cut a bagel into a trefoil knot for some "mathematically correct breakfast" - link  

Images 2 and 5 from here, Image 3 from here, and Image 4 from here.

Mathematical Broccoli

This is hands down my new favorite vegetable. It's called Romanesco broccoli and I'd seen pictures of it online (it's also mentioned in Benoit Mandelbrot's TED talk here) but never in person until tonight. Isn't it just gorgeous though? It approximates a fractal in that it is a pattern that repeats itself infinitely...or well, as far as the physical limits of broccoli allow, that is. If you were to cut off one of the little florets, it would look like a copy of the whole thing, but smaller. Also of interest is that the little buds are arranged in logarithmic spirals, and like pinecones, counting the number of spirals going one way and then going the other way results in adjacent Fibonacci numbers. 

Seriously, can we just admire how intricate and awesome this broccoli is?!

Image source.

Twisted Tessellations II - Reflection

Original artwork by M. C. Escher. Image source. In addition to translations, another type of tessellation is a reflection, where a shape has been flipped about either the x or y axis. 

Step 1 - Like for translations, start with a square piece of paper. Now pick one edge, mark off the midpoint, and draw some kind of squiggle from the corner to the center point. 

Step 2 - Cut out the piece you've just drawn, flip it over, and line it up with the other half of the chosen edge. Trace and cut out. Now you'll have two little pieces that are reflections of each other. 

Step 3 - Take those two pieces and line them up on the opposite edge as shown. Trace and cut out.

Step 4 - Attach the four pieces you've cut out to the two uncut edges like so. If you've done this correctly, you'll be able to draw a line right down the middle both horizontally and vertically and have the two sides be mirror images of one another. 

Now your beautiful stencil is ready to trace! 

Notice how, because of the symmetry, it doesn't matter which side is facing up.

This pattern also has some neat rotational symmetry, but that's another story...

Twisted Tessellations I - Translation

This delightful tessellation I found on an intricately decorated door has inspired a four-part series on drawing the various types of tessellations. The word "tessellation" comes from the Latin tessella, which is a small square tile of stone or glass used to make mosaics. Thus a tessellation is a tiling of a plane using geometric shapes with no overlaps or gaps. 

Original artwork by M. C. Escher. Image source. One type of tessellation is called a translation. Here, the shape is simply translated, or slid, across the plane and drawn again. And now, a fairly easy way to create translation tessellations of your own.  

Step 1 - Take a square piece of paper (this is a 2" x 2" square) and draw any sort of squiggle that you want. Thicker paper works better because we're going to be using it like a stencil later on; here I'm using colorful index cards. 

Step 2 - Cut out the squiggly bit. 

 

 Step 3 - Slide the squiggly bit down and tape it to the edge opposite the one you cut it from.  

Step 4 - Pick one of the remaining two sides and draw another squiggle. 

Step 5 - Repeat Step 3 with the second squiggly bit. 

Step 6 - Now your stencil is ready to use. Hold the shape still on a piece of paper and trace around it. 

You can now continue the pattern by sliding the whole shape up or down/left or right and lining it up with the already drawn edge and tracing again. 

This super simple method can be continued on forever and you can expand your tessellation indefinitely (or until you run out of paper, whichever comes first). 

Visualizing Solids of Revolution

A project two of my friends and I did for our Multivariable class, showing different visualizations, examples, and applications of finding the volume of a solid of revolution using disks, washers, and shells - a concept we learned last year. 

Fibonnaci Pinecone

So I really like pinecones - I have a bunch just lying around my room because I find them very spirally and pretty. But in addition to that, they're beautifully mathematical. All you have to do is count the number of spirals; this pinecone has 8 going this way... 

And 13 the other way. Two of my other pinecones have 3 spirals and 5 spirals, and 5 and 8 spirals. Sound familiar? These are adjacent Fibonacci numbers - seriously, the series you get by adding the two previous numbers that goes 1, 1, 2, 3, 5, 8, 13, 21, 34... shows up everywhere in nature, from sunflower seeds to artichokes to pineapples. This is because these Fibonacci arrangements result in the optimal packing of seeds/leaves/plant bits, so that they are all uniformly spaced and can maximize the amount of sunlight they receive. The more you look for these instances of Fibonacci numbers in the world around you, the more you'll find them - delightful glimpses into the mathematics in which our universe is written.